Carleman matrix
In mathematics, a Carleman matrix is a matrix that is used to convert function composition into matrix multiplication. They are used in iteration theory to find the continuous iteration of functions that cannot be iterated by pattern recognition alone. Other uses of Carleman matrices are in the theory of probability generating functions, and Markov chains.
Contents |
Definition
The Carleman matrix of a function  is defined as:
is defined as:
so as to satisfy the equation:
So for instance we have the computation of  by
by
which is simply the dot-product of row 1 of ![M[f]](/2012-wikipedia_en_all_nopic_01_2012/I/f4b94b35f522952a0f224d3a59b8a80f.png) by a columnvector
by a columnvector ![\left[1,x,x^2,x^3,...\right]^\tau](/2012-wikipedia_en_all_nopic_01_2012/I/8f8620b120910c68eb7b2402d889d149.png)
The entries of ![M[f]](/2012-wikipedia_en_all_nopic_01_2012/I/f4b94b35f522952a0f224d3a59b8a80f.png) of the next row give the 2nd power of
of the next row give the 2nd power of  :
:
and also, for to have the zero'th power of  in
in ![M[f]](/2012-wikipedia_en_all_nopic_01_2012/I/f4b94b35f522952a0f224d3a59b8a80f.png) we assume the row 0 containing zeros everywhere except the first position, such that
we assume the row 0 containing zeros everywhere except the first position, such that
Thus the dot-product of ![M[f]](/2012-wikipedia_en_all_nopic_01_2012/I/f4b94b35f522952a0f224d3a59b8a80f.png) with the column-vector
with the column-vector ![\left[1,x,x^2,...\right]^\tau](/2012-wikipedia_en_all_nopic_01_2012/I/8a723a0e26c5f60a9c4c958632e3e2e5.png) gives the columnvector
gives the columnvector ![\left[1,f(x),f(x)^2,...\right]^\tau](/2012-wikipedia_en_all_nopic_01_2012/I/df3172ad7b871bcda5b5209094522ff5.png)
Bell matrix
The Bell matrix of a function  is defined as:
is defined as:
so as to satisfy the equation:
which means it is basically the transpose of the Carleman matrix.
Generalization
A generalization of the Carleman matrix of a function can be defined around any point, such as:
or ![M[f]_{x_0} = M[g]](/2012-wikipedia_en_all_nopic_01_2012/I/e244efea547421b71ae2d58f5a8c5551.png) where
where 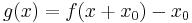 . This allows the matrix power to be related as:
. This allows the matrix power to be related as:
Matrix properties
These matrices satisfy the fundamental relationships:
which makes the Carleman matrix M a (direct) representation of  , and the Bell matrix B an anti-representation of
, and the Bell matrix B an anti-representation of  . Here the term
. Here the term 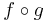 means the composition of functions
means the composition of functions 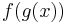
Other properties include:
![\,M[f^n] = M[f]^n](/2012-wikipedia_en_all_nopic_01_2012/I/81fad4cea59721f65dc89707302a6304.png) , where
, where 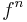 is function iteration and
is function iteration and![\,M[f^{-1}] = M[f]^{-1}](/2012-wikipedia_en_all_nopic_01_2012/I/cb4d25ae00cd07a3d18d71f079a892ce.png) , where
, where 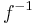 is the inverse function (if the Carleman matrix is invertible).
is the inverse function (if the Carleman matrix is invertible).
Examples
The Carleman matrix of a constant is:
The Carleman matrix of the identity function is:
The Carleman matrix of a constant addition is:
The Carleman matrix of a constant multiple is:
The Carleman matrix of a linear function is:
The Carleman matrix of a function 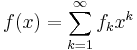 is:
is:
The Carleman matrix of a function 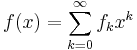 is:
is:
See also
References
- R Aldrovandi, Special Matrices of Mathematical Physics: Stochastic, Circulant and Bell Matrices, World Scientific, 2001. (preview)
- R. Aldrovandi, L. P. Freitas, Continuous Iteration of Dynamical Maps, online preprint, 1997.
- P. Gralewicz, K. Kowalski, Continuous time evolution from iterated maps and Carleman linearization, online preprint, 2000.
- K Kowalski and W-H Steeb, Nonlinear Dynamical Systems and Carleman Linearization, World Scientific, 1991. (preview)
![M[f]_{jk} = \frac{1}{k!}\left[\frac{d^k}{dx^k} (f(x))^j \right]_{x=0}](/2012-wikipedia_en_all_nopic_01_2012/I/faa9412fa354389682022a7a0ff40abb.png)
![(f(x))^j = \sum_{k=0}^{\infty} M[f]_{jk} x^k.](/2012-wikipedia_en_all_nopic_01_2012/I/284c2db31e08a87eb02a52e577d9c239.png)
![f(x) = \sum_{k=0}^{\infty} M[f]_{1,k} x^k.](/2012-wikipedia_en_all_nopic_01_2012/I/b659227dacc4530d0be5343d8b01f5de.png)
![f(x)^2 = \sum_{k=0}^{\infty} M[f]_{2,k} x^k.](/2012-wikipedia_en_all_nopic_01_2012/I/b3fd0330d26b8a55ef8921c35ef93fea.png)
![f(x)^0 = 1 = \sum_{k=0}^{\infty} M[f]_{0,k} x^k = 1%2B \sum_{k=1}^{\infty} 0* x^k](/2012-wikipedia_en_all_nopic_01_2012/I/c98e924c5a50e13c8f921f3881fd8a70.png)
![M[f] * \left[ 1,x,x^2,x^3,...\right]^\tau = \left[ 1,f(x),(f(x))^2,(f(x))^3,...\right]^\tau.](/2012-wikipedia_en_all_nopic_01_2012/I/dbe655cfaeaf84a1396ebebd0a1de54d.png)
![B[f]_{jk} = \frac{1}{j!}\left[\frac{d^j}{dx^j} (f(x))^k \right]_{x=0}](/2012-wikipedia_en_all_nopic_01_2012/I/b8faff5e4797bbe1add3ea47e64b2ec4.png)
![(f(x))^k = \sum_{j=0}^{\infty} B[f]_{jk} x^j](/2012-wikipedia_en_all_nopic_01_2012/I/406cc50e97e3aa2f2298c223fd7e28e3.png)
![M[f]_{x_0} = M_x[x - x_0]M[f]M_x[x %2B x_0]](/2012-wikipedia_en_all_nopic_01_2012/I/b51a57b4ba27bd9da6e6ad85b894a83a.png)
![(M[f]_{x_0})^n = M_x[x - x_0]M[f]^nM_x[x %2B x_0]](/2012-wikipedia_en_all_nopic_01_2012/I/c35a6f2b998fec92d42b41ec850951dc.png)
![M[f \circ g] = M[f]M[g]](/2012-wikipedia_en_all_nopic_01_2012/I/34b396f0776a2a860cac11bf468ce3a7.png)
![B[f \circ g] = B[g]B[f]](/2012-wikipedia_en_all_nopic_01_2012/I/6f7c04bba384cbd6a2b177baa8a6dc19.png)
![M[a] = \left(\begin{array}{cccc}
1&0&0& \cdots \\
a&0&0& \cdots \\
a^2&0&0& \cdots \\
\vdots&\vdots&\vdots&\ddots
\end{array}\right)](/2012-wikipedia_en_all_nopic_01_2012/I/b5a65dfd3e2157a40199313e2cfd8886.png)
![M_x[x] = \left(\begin{array}{cccc}
1&0&0& \cdots \\
0&1&0& \cdots \\
0&0&1& \cdots \\
\vdots&\vdots&\vdots&\ddots
\end{array}\right)](/2012-wikipedia_en_all_nopic_01_2012/I/4feec05c94457d54d8f1519e86fbfb47.png)
![M_x[a %2B x] = \left(\begin{array}{cccc}
1&0&0& \cdots \\
a&1&0& \cdots \\
a^2&2a&1& \cdots \\
\vdots&\vdots&\vdots&\ddots
\end{array}\right)](/2012-wikipedia_en_all_nopic_01_2012/I/19da4de463586d1806c8442aa59e4fff.png)
![M_x[cx] = \left(\begin{array}{cccc}
1&0&0& \cdots \\
0&c&0& \cdots \\
0&0&c^2& \cdots \\
\vdots&\vdots&\vdots&\ddots
\end{array}\right)](/2012-wikipedia_en_all_nopic_01_2012/I/015d31f2cd1633286b63dd55c1aad730.png)
![M_x[a %2B cx] = \left(\begin{array}{cccc}
1&0&0& \cdots \\
a&c&0& \cdots \\
a^2&2ac&c^2& \cdots \\
\vdots&\vdots&\vdots&\ddots
\end{array}\right)](/2012-wikipedia_en_all_nopic_01_2012/I/04d219a3c8a1ad39adf849c3f3534f60.png)
![M[f] = \left(\begin{array}{cccc}
1&0&0& \cdots \\
0&f_1&f_2& \cdots \\
0&0&f_1^2& \cdots \\
\vdots&\vdots&\vdots&\ddots
\end{array}\right)](/2012-wikipedia_en_all_nopic_01_2012/I/c67b4e2f05af527885e3885dd6c823bb.png)
![M[f] = \left(\begin{array}{cccc}
1&0&0& \cdots \\
f_0&f_1&f_2& \cdots \\
f_0^2&2f_0f_1&f_1^2& \cdots \\
\vdots&\vdots&\vdots&\ddots
\end{array}\right)](/2012-wikipedia_en_all_nopic_01_2012/I/c0a4e74ac023ecc0490d61dee95e9104.png)